#include <disthals.hpp>

Public Member Functions
	DistHALS (const INPUTMATTYPE &input, const MAT &leftlowrankfactor, const MAT &rightlowrankfactor, const MPICommunicator &communicator, const int numkblks)

void	distWtA ()
	This is a matrix multiplication routine based on reduce_scatter. More...

void	distWtABlock ()

void	distAH ()
	There are totally prxpc process. More...

void	distAHBlock ()

void	distInnerProduct (const MAT &X, MAT *XtX)
	There are p processes. More...

void	computeNMF ()
	This is the main loop function Refer Algorithm 1 in Page 3 of the PPoPP HPC-NMF paper. More...

void	computeError (const int it)
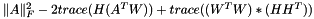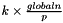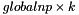	We assume this error function will be called in every iteration before updating the block to compute the error from previous iteration $\\|A\\|_F^2 - 2trace(H(A^TW))+trace((W^TW)(HH^T))$ each process owns globalsqnormA will have \|A\|_F^2 each process owns WtAij is of size $k \times \frac{globaln}{p}$ each process owns H is of size ${globaln}{p} \times k$ compute WtAijH and do an MPI_ALL reduce to get the kxk matrix. More...

void	computeError2 (const int it)

const int	globalm () const
	returns globalm More...

const int	globaln () const
	returns globaln More...

const double	globalsqnorma () const
	returns global squared norm of A More...

void	compute_error (const uint &ce)
	return the current error More...

const bool	is_compute_error () const
	returns the flag to compute error or not. More...

void	algorithm (algotype dat)
	returns the NMF algorithm More...

void	reportTime (const double temp, const std::string &reportstring)
	Reports the time. More...

void	normalize_by_W ()
	Column Normalizes the distributed W matrix. More...

MAT	getLeftLowRankFactor ()
	Returns the left low rank factor matrix W. More...

MAT	getRightLowRankFactor ()
	Returns the right low rank factor matrix H. More...

void	computeObjectiveError ()

void	computeObjectiveError (const INPUTMATTYPE &At, const MAT &WtW, const MAT &HtH)

void	num_iterations (const int it)
	Sets number of iterations for the NMF algorithms. More...

const unsigned int	num_iterations () const
	Returns the number of iterations. More...

void	regW (const FVEC &iregW)
	Sets the regularization on left low rank factor W. More...

FVEC	regW ()
	Returns the L2 and L1 regularization parameters of W as a vector. More...

void	regH (const FVEC &iregH)
	Sets the regularization on right low rank H. More...

FVEC	regH ()
	Returns the L2 and L1 regularization parameters of W as a vector. More...

void	clear ()
	Clear the memory for input matrix A, right low rank factor W and left low rank factor H. More...

Detailed Description

template<class INPUTMATTYPE>
class planc::DistHALS< INPUTMATTYPE >

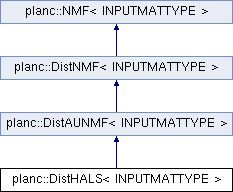
Definition at line 16 of file disthals.hpp.

Inheritance diagram for planc::DistHALS< INPUTMATTYPE >:

Constructor & Destructor Documentation

◆ DistHALS()

template<class INPUTMATTYPE>

planc::DistHALS< INPUTMATTYPE >::DistHALS	(	const INPUTMATTYPE &	input,
		const MAT &	leftlowrankfactor,
		const MAT &	rightlowrankfactor,
		const MPICommunicator &	communicator,
		const int	numkblks
	)

inline

Definition at line 97 of file disthals.hpp.

Member Function Documentation

◆ algorithm()

template<typename INPUTMATTYPE >

void planc::DistNMF< INPUTMATTYPE >::algorithm ( algotype dat )

inlineinherited

returns the NMF algorithm

Definition at line 94 of file distnmf.hpp.

◆ clear()

void planc::NMF< INPUTMATTYPE >::clear ( )

inlineinherited

Clear the memory for input matrix A, right low rank factor W and left low rank factor H.

Definition at line 355 of file nmf.hpp.

◆ compute_error()

template<typename INPUTMATTYPE >

void planc::DistNMF< INPUTMATTYPE >::compute_error ( const uint & ce )

inlineinherited

return the current error

Definition at line 90 of file distnmf.hpp.

◆ computeError()

template<class INPUTMATTYPE >

void planc::DistAUNMF< INPUTMATTYPE >::computeError ( const int it )

inlineinherited

We assume this error function will be called in every iteration before updating the block to compute the error from previous iteration 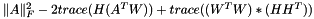$\|A\|_F^2 - 2trace(H(A^TW))+trace((W^TW)*(HH^T))$ each process owns globalsqnormA will have |A|_F^2 each process owns WtAij is of size 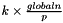$k \times \frac{globaln}{p}$ each process owns H is of size 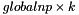${globaln}{p} \times k$ compute WtAij*H and do an MPI_ALL reduce to get the kxk matrix.

every process local computation

Definition at line 540 of file aunmf.hpp.

◆ computeError2()

template<class INPUTMATTYPE >

void planc::DistAUNMF< INPUTMATTYPE >::computeError2 ( const int it )

inlineinherited

Definition at line 570 of file aunmf.hpp.

◆ computeNMF()

template<class INPUTMATTYPE >

void planc::DistAUNMF< INPUTMATTYPE >::computeNMF ( )

inlinevirtualinherited

This is the main loop function Refer Algorithm 1 in Page 3 of the PPoPP HPC-NMF paper.

Implements planc::NMF< INPUTMATTYPE >.

Definition at line 415 of file aunmf.hpp.

◆ computeObjectiveError() [1/2]

void planc::NMF< INPUTMATTYPE >::computeObjectiveError ( )

inlineinherited

Definition at line 238 of file nmf.hpp.

◆ computeObjectiveError() [2/2]

void planc::NMF< INPUTMATTYPE >::computeObjectiveError	(	const INPUTMATTYPE &	At,
		const MAT &	WtW,
		const MAT &	HtH
	)

inlineinherited

Definition at line 330 of file nmf.hpp.

◆ distAH()

template<class INPUTMATTYPE >

void planc::DistAUNMF< INPUTMATTYPE >::distAH ( )

inlineinherited

There are totally prxpc process.

Each process will hold the following An A of size (m/pr) x (n/pc) H of size (n/p)xk find AHt kx(m/p) by reducing and scatter it using MPI_Reduce_scatter call. That is, p process will hold a kx(m/p) matrix. this->m_mpicomm.comm_subs()[0] is column communicator. this->m_mpicomm.comm_subs()[1] is row communicator. To preserve the memory for Hj, we collect only partial k

Definition at line 292 of file aunmf.hpp.

◆ distAHBlock()

template<class INPUTMATTYPE >

void planc::DistAUNMF< INPUTMATTYPE >::distAHBlock ( )

inlineinherited

Definition at line 301 of file aunmf.hpp.

◆ distInnerProduct()

template<class INPUTMATTYPE >

void planc::DistAUNMF< INPUTMATTYPE >::distInnerProduct	(	const MAT &	X,
		MAT *	XtX
	)

inlineinherited

There are p processes.

Every process i has W in m_i * k At the end of this call, all process will have WtW of size k*k is symmetric. So not to worry about column/row major formats.

Parameters

[in]	X	is of size m_i x k
[out]	XtX	Every process owns the same kxk global gram matrix of X

Definition at line 386 of file aunmf.hpp.

◆ distWtA()

template<class INPUTMATTYPE >

void planc::DistAUNMF< INPUTMATTYPE >::distWtA ( )

inlineinherited

This is a matrix multiplication routine based on reduce_scatter.

A is mxn in column major ordering W is mxk in column major ordering AtW is nxk in column major ordering There are totally p processes. Every process has A_i as m_i * n W_i as m_i * k AtW_i as n_i * k this->m_mpicomm.comm_subs()[0] is column communicator. this->m_mpicomm.comm_subs()[1] is row communicator.

Definition at line 205 of file aunmf.hpp.

◆ distWtABlock()

template<class INPUTMATTYPE >

void planc::DistAUNMF< INPUTMATTYPE >::distWtABlock ( )

inlineinherited

Definition at line 214 of file aunmf.hpp.

◆ getLeftLowRankFactor()

MAT planc::NMF< INPUTMATTYPE >::getLeftLowRankFactor ( )

inlineinherited

Returns the left low rank factor matrix W.

Definition at line 167 of file nmf.hpp.

◆ getRightLowRankFactor()

MAT planc::NMF< INPUTMATTYPE >::getRightLowRankFactor ( )

inlineinherited

Returns the right low rank factor matrix H.

Definition at line 169 of file nmf.hpp.

◆ globalm()

template<typename INPUTMATTYPE >

const int planc::DistNMF< INPUTMATTYPE >::globalm ( ) const

inlineinherited

returns globalm

Definition at line 84 of file distnmf.hpp.

◆ globaln()

template<typename INPUTMATTYPE >

const int planc::DistNMF< INPUTMATTYPE >::globaln ( ) const

inlineinherited

returns globaln

Definition at line 86 of file distnmf.hpp.

◆ globalsqnorma()

template<typename INPUTMATTYPE >

const double planc::DistNMF< INPUTMATTYPE >::globalsqnorma ( ) const

inlineinherited

returns global squared norm of A

Definition at line 88 of file distnmf.hpp.

◆ is_compute_error()

template<typename INPUTMATTYPE >

const bool planc::DistNMF< INPUTMATTYPE >::is_compute_error ( ) const

inlineinherited

returns the flag to compute error or not.

Definition at line 92 of file distnmf.hpp.

◆ normalize_by_W()

template<typename INPUTMATTYPE >

void planc::DistNMF< INPUTMATTYPE >::normalize_by_W ( )

inlineinherited

Column Normalizes the distributed W matrix.

Definition at line 110 of file distnmf.hpp.

◆ num_iterations() [1/2]

void planc::NMF< INPUTMATTYPE >::num_iterations ( const int it )

inlineinherited

Sets number of iterations for the NMF algorithms.

Definition at line 340 of file nmf.hpp.

◆ num_iterations() [2/2]

const unsigned int planc::NMF< INPUTMATTYPE >::num_iterations ( ) const

inlineinherited

Returns the number of iterations.

Definition at line 350 of file nmf.hpp.

◆ regH() [1/2]

void planc::NMF< INPUTMATTYPE >::regH ( const FVEC & iregH )

inlineinherited

Sets the regularization on right low rank H.

Definition at line 344 of file nmf.hpp.

◆ regH() [2/2]

FVEC planc::NMF< INPUTMATTYPE >::regH ( )

inlineinherited

Returns the L2 and L1 regularization parameters of W as a vector.

Definition at line 348 of file nmf.hpp.

◆ regW() [1/2]

void planc::NMF< INPUTMATTYPE >::regW ( const FVEC & iregW )

inlineinherited

Sets the regularization on left low rank factor W.

Definition at line 342 of file nmf.hpp.

◆ regW() [2/2]

FVEC planc::NMF< INPUTMATTYPE >::regW ( )

inlineinherited

Returns the L2 and L1 regularization parameters of W as a vector.

Definition at line 346 of file nmf.hpp.

◆ reportTime()

template<typename INPUTMATTYPE >

void planc::DistNMF< INPUTMATTYPE >::reportTime	(	const double	temp,
		const std::string &	reportstring
	)

inlineinherited

Reports the time.

Definition at line 96 of file distnmf.hpp.

The documentation for this class was generated from the following file:

/Users/rnu/Documents/research/nmflibrary/distnmf/disthals.hpp

Public Member Functions

Detailed Description

template<class INPUTMATTYPE> class planc::DistHALS< INPUTMATTYPE >

Constructor & Destructor Documentation

◆ DistHALS()

Member Function Documentation

◆ algorithm()

◆ clear()

◆ compute_error()

◆ computeError()

◆ computeError2()

◆ computeNMF()

◆ computeObjectiveError() [1/2]

◆ computeObjectiveError() [2/2]

◆ distAH()

◆ distAHBlock()

◆ distInnerProduct()

◆ distWtA()

◆ distWtABlock()

◆ getLeftLowRankFactor()

◆ getRightLowRankFactor()

◆ globalm()

◆ globaln()

◆ globalsqnorma()

◆ is_compute_error()

◆ normalize_by_W()

◆ num_iterations() [1/2]

◆ num_iterations() [2/2]

◆ regH() [1/2]

◆ regH() [2/2]

◆ regW() [1/2]

◆ regW() [2/2]

◆ reportTime()

template<class INPUTMATTYPE>
class planc::DistHALS< INPUTMATTYPE >