planc Namespace Reference

ncp_factors contains the factors of the ncp every ith factor is of size n_i * k number of factors is called as mode of the tensor all idxs are zero idx. More...

Classes
class	AOADMMNMF
class	AUNTF
class	BPPNMF
class	DistALS
class	DistANLSBPP
class	DistAOADMM
class	DistAUNMF
class	DistAUNTF
class	DistHALS
class	DistIO
class	DistMU
class	DistNaiveANLSBPP
class	DistNMF
class	DistNMF1D
class	DistNMFDriver
class	DistNMFTime
class	DistNTF
class	DistNTFANLSBPP
class	DistNTFAOADMM
class	DistNTFCPALS
class	DistNTFHALS
class	DistNTFIO
class	DistNTFMU
class	DistNTFNES
class	DistNTFTime
class	HALSNMF
class	MPICommunicator
class	MUNMF
class	NCPFactors
class	NMF
class	NTFANLSBPP
class	NTFAOADMM
class	NTFDriver
class	NTFHALS
class	NTFMPICommunicator
class	NTFMU
class	NTFNES
class	NumPyArray
class	ParseCommandLine
class	Tensor
	Data is stored such that the unfolding 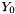is column major. More...

Detailed Description

ncp_factors contains the factors of the ncp every ith factor is of size n_i * k number of factors is called as mode of the tensor all idxs are zero idx.

Tensor A of size is M1 x M2 x...

Class and function for 2D MPI communicator with row and column communicators.

Class and function for collecting time statistics.

Distributed MU factorization.

File name formats A is the filename 1D distribution Arows_totalpartitions_rank or Acols_totalpartitions_rank Double 1D distribution (both row and col distributed) Arows_totalpartitions_rank and Acols_totalpartitions_rank TWOD distribution A_totalpartition_rank Just send the first parameter Arows and the second parameter Acols to be zero.

emulating Jingu's code https://github.com/kimjingu/nonnegfac-matlab/blob/master/nmf.m function hals_iterSolver

Unconstrained least squares.

There are totally prxpc process.

Each process will hold the following An A of size 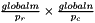Here each process 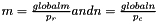H of size 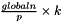W of size 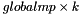A is 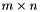matrix H is 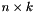matrix

Should match the SVD objective error.

Offers implementation for the pure virtual function updateW and updateH based on MU.

x Mn is distributed among P1 x P2 x ... x Pn grid of P processors. That means, every processor has (M1/P1) x (M2/P2) x ... x (Mn/Pn) tensor as m_input_tensor. Similarly every process own a portion of the factors as H(i,pi) of size (Mi/Pi) x k and collects from its neighbours as H(i,p) as (Mi/P) x k H(i,p) and m_input_tensor can perform local MTTKRP. The local MTTKRP's are reduced scattered for local NNLS.